点击宏观经济研学会关注我们
?All is Study, All is Research?
许文立，CIMERS，cimers_dsge@econmod.cn
Higher?Oder Approximation?of DSGE
全文约2800字
预计需12分钟阅读全文
为什么要做高阶近似？（1）福利分析；（2）更精确；（3）状态依赖效应；（4）不确定性冲击。经验数据显示较大规模的冲击时，高阶近似可能会“爆炸(explosion)”。通常，我们会：（1）减少冲击规模；（2）采用pruning；还有一种方式（3）非线性移动平均（NLMA）。今天，我们就给大家介绍一下这些方法及code的用法。
正
文
金融危机后，人们越来越认识到宏观经济的非线性效应。DSGE模型也不像过去一样用一阶近似，而更多的使用高阶近似。
Dynare中现在也可以使用高阶近似（基于2阶和3阶近似）。高阶近似有许多好处：
（1）对于福利分析来说，用高阶近似更加恰当，参见【免费下载】Dynare v4.5 - User Guide for Advanced Topics中的福利分析章节；
（2）高阶近似更加精确；
（3）高阶近似允许我们来研究状态依存效应，即脉冲响应依赖于冲击发生时的初始状态；
（4）如果我们想要研究不确定性冲击（即外生冲击方差的冲击，二阶矩冲击），就必须用到3阶近似。
?
但是，我们在做高阶近似的时候，可能会出现高阶状态空间表达式的系数“爆炸”（explosion）的情况。那么，这个时候，我们怎么计算脉冲响应，并得到模拟结果呢？
今天就为大家提供几种解决方案。
一、模型
本文的基准模型来自E. Sims（2017）：“Using Dynare”。

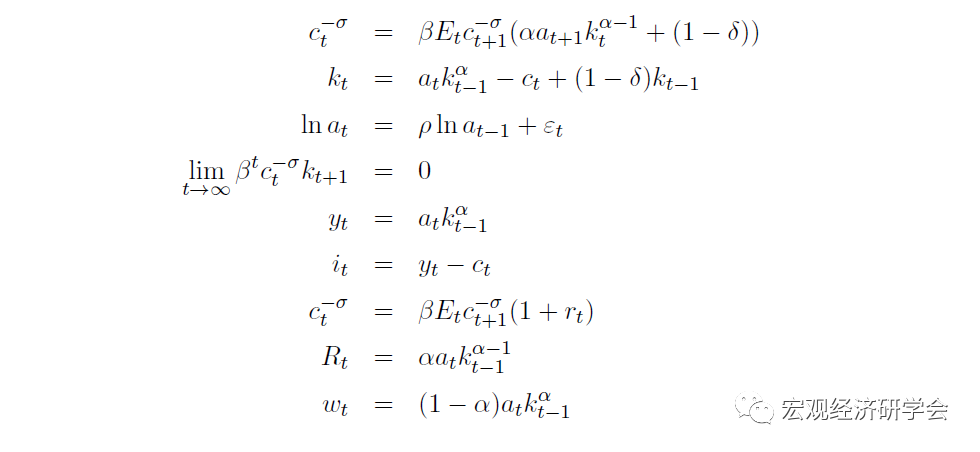
其中，变量名称都为常规经济指标。极限为横截条件。
DSGE的模型构建与推导，经济含义参见往期“DSGE建模与编程汇总”。
二、Dynare code
% Higher order approximation:% (1) reducing size of shocks% (2)pruning% (3)NLMA—nonlinear maving aerage
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% the template is based on the model in Sims' "Using Dynare"% @Wenddy Xu,CIMERS, xuweny87@163.com
var y I k a c w R r;varexo e;parameters alpha beta delta rho sigma sigmae;
alpha=1/3;beta=0.99;delta=0.025;rho=0.95;sigma=1;sigmae=1; % 冲击的标准差
model;
exp(c)^(-sigma)=beta*exp(c(1))^(-sigma)*(alpha*exp(a(1))*exp(k)^(alpha-1)+(1-delta));
exp(y) = exp(a)*exp(k(-1))^(alpha);exp(k) = exp(a)*exp(k(-1))^(alpha)-exp(c) + (1-delta)*exp(k(-1));a = rho*a(-1) + e;exp(y) = exp(c) + exp(I);exp(c)^(-sigma) = beta*exp(c(+1))^(-sigma)*(1+r);exp(R) = alpha*exp(a)*exp(k(-1))^(alpha-1);exp(w) = (1-alpha)*exp(a)*exp(k(-1))^(alpha);
end;
initval;k = log(30);y = log(3);c = log(2.5);I = log(0.5);a = 0;r = (1/beta)-1;R = log((1/beta)-(1-delta));w = log(1);end;
shocks;var?e?=?sigmae^2;??%?外生冲击e的方差end;
steady;
stoch_simul(order=2,irf=40);
如果我们直接运行上述dynare code，matlab不会显示脉冲相应图(IRFs)，并提示：
stoch_simul: The simulations conducted for generating IRFs to e were explosive.stoch_simul: No IRFs will be displayed. Either reduce the shock size, stoch_simul:?use?pruning,?or?set?the?approximation?order?to?1.
上面这个提示信息就表示，我们在对模型进行2阶近似的时候，状态空间表达式的系数出现“爆炸”。Dynare的提示已经给出了三种解决方案：
（1）将模型近似阶数设置为1，即order=1。可是，正如本讲的目的，我们就是想做高阶近似，那怎么办？
（2）降低冲击规模；
%?我们可以看看上述代码的19行和47行：sigmae=1; % 冲击的标准差
var e = sigmae^2; % 外生冲击e的方差
此处设置的冲击规模sigmae=1表示外生冲击的方差为1，其冲击规模太大。我们可以降低该值，例如，sigmae=0.01，来解决上述“爆炸”问题。
% 我们可以看看上述代码的19行和47行：sigmae=0.01; % 冲击的标准差
var e = sigmae^2; % 外生冲击e的方差
问题在于，外生冲击的规模可能是我们根据我国实际数据计算得到的。也就是说，在某些时候，我国的技术冲击方差就是1。那么，降低冲击规模肯定不合适，这个时候怎么办？
（3）Dynare还提供了另一种解决方案：使用stoch_simul(pruning)；也就是说，将上述代码的第50行改为：
stoch_simul(order=2,irf=40,pruning);
这时，我们可以得到脉冲响应结果：

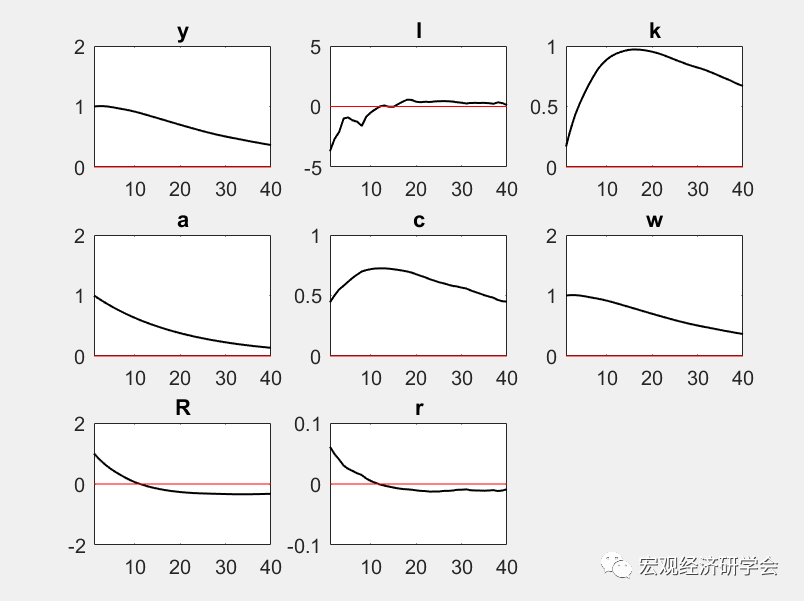
下面，我们来看看“pruning”背后的机制：
以一个二次型一阶自回归过程为例（注：DSGE在二阶近似下得到的缩减形式解有更多项）：
yt=ρyt-1^2
给定初值为y0，那么，
y1=ρy0^2
y2=ρ^3y0^4
……
这里，我们可能就有点熟悉了。因为|ρ|<1，上述AR过程似乎是平稳过程。为什么是似乎？因为上述过程产生的路径仍有可能是发散的，这还依赖于初始状态y0。如果|y0|>1，那么，上述过程就是发散的！
当我们在处理非线性模型时，动态路径依赖于历史是常常会遇到的问题。但是，Dynare在处理非线性DSGE的情况变得更坏，这是由于对原始模型用扰动法得到的近似。
而pruning法就是尝试消除与初始条件相关的“爆炸”问题。pruning是丢弃二阶以上的近似项。这个想法是由Kim，kim，Schaumburg and Sims（2008）提出来的。
假设真实模型为：
yt=Γyt-1+ρyt-1^2
pruning法是由另一个状态变量扩增形式组成，另一个状态变量则是由真是模型的线性部分定义：
zt=Γzt-1
且z0=y0。这个模型就转变成：
yt=Γyt-1+ρzt-1^2
zt=Γzt-1
很明显，上述系统产生的动态路径与原始模型的路径不同。但是只要新的变量zt是平稳的，上述系统就是平稳的。路径并不依赖于初始条件。
pruning虽然可以解决高阶近似“爆炸”问题，但它也存在问题：正如上文提及的，pruning改变了原始模型，也就是说，我们用pruning得到的脉冲响应实际上并不是原始模型的脉冲响应。de Haan（2016）指出，pruning会使得扰动解产生非常大的扭曲。
（4）除了上面三种解决方案外，还有第四中方法来解决上述问题。那就是Lan and Meyer-Gohde（2013，JECD)提出的非线性移动平均（NLMA）近似。
首先，去Lan Hongken的Github（https://github.com/lanhongken/nlma）下载NLMA工具包。
然后，将nlma文件夹放到Dynare的contrib文件里：
C:\dynare\4.5.7\contrib\nlma %对应自己电脑的文件夹路径再然后，将上述路径增加到Matlab的工作路径中：
>> addpath C:\dynare\4.5.7\contrib\nlma最后，我们只需要在上述MOD文件的最后加上nlma代码即可：
stoch_simul(order=2,irf=0);
options_.irf = 40;
nlma_irf?=?nlma_irf(M_,options_,var_list_);
上述代码中，我们需要将stoch_simul中的irf=0，这是不让dynare产生脉冲相应图；然后设置options_.irf=40;用nlma_irf来调用nlma工具箱计算并画出二阶脉冲响应图。这个时候，MATLAB就会给出所有内生变量的脉冲相应图。例如：

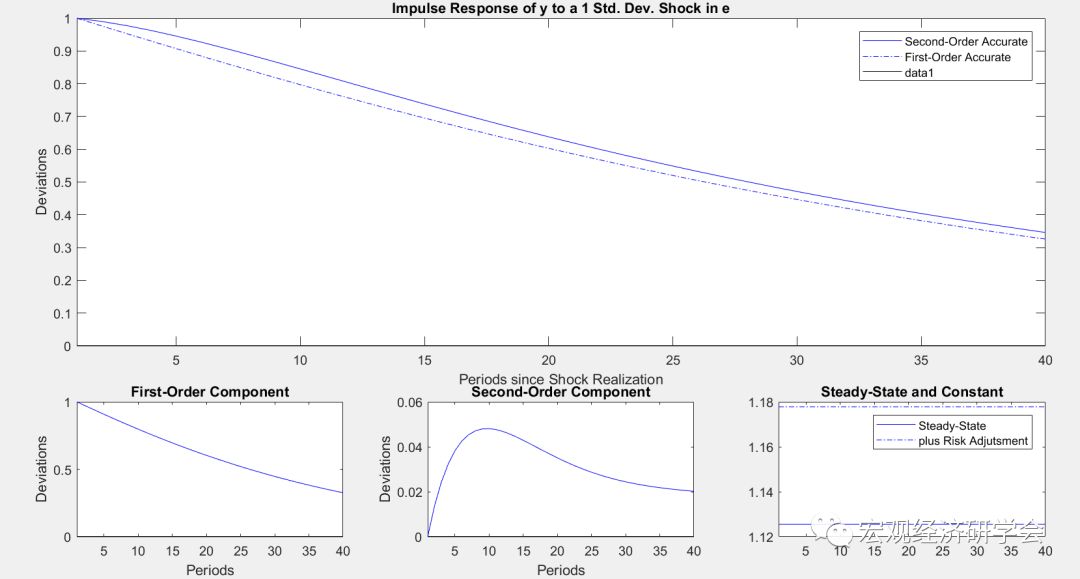
由于NLMA工具箱会分别画出DSGE模型中每一个内生变量的脉冲相应图，对于大型模型来说，内生变量较多。因此，建议在stoch_simul命令后加上我们感兴趣的内生变量名：
stoch_simul(order=2,irf=0)y?I?c;?%这时候只会画出y，I，c的脉冲相应图
options_.irf = 40;
nlma_irf?=?nlma_irf(M_,options_,var_list_);
NLMA算法的理论细节请参见Lan and Meyer-Gohde(2013,JEDC)。
值得一提的是，在下下一代Dynare 5.0中将合并nlma。也就是说，在Dynare 5.0中，我们将在高阶近似的stoch_simul中见到选项nlma，因此，今天的推文相当于是提前体验一下Dynare 5.0的功能。
（1）推荐阅读Dynare手册和Lan and Meyer-Gohde（2013，JECD），支持原创研究
（2）上述代码，上传到“定量经济分析平台”www.econmod.cn。可免费注册下载！引用请注明来源！
THE END
●图片贴纸来源 | 秀米IUMI
●排版 |?许坤，卢倩倩
长按 关注公众号
?CIMERS_DSGE
长按识别二维码，关注我们
回复关键词：DSGE | R
声明：我们欢迎读者朋友通过留言的方式与作者交流使用心得以及探讨研究合作；同时，为支持知识产权保护，本文在任何情形下均不得用于商业目的。